Diffraction tomography with a deep image prior
Optics Express (2020)
Kevin C. Zhou and Roarke Horstmeyer
Department of Biomedical Engineering, Duke University, Durham, NC 27708
Links to paper, code, and data.
Abstract
We present a tomographic imaging technique, termed Deep Prior Diffraction Tomography (DP-DT), to reconstruct the 3D refractive index (RI) of thick biological samples at high resolution from a sequence of low-resolution images collected under angularly varying illumination. DP-DT processes the multi-angle data using a phase retrieval algorithm that is extended by a deep image prior (DIP), which reparameterizes the 3D sample reconstruction with an untrained, deep generative 3D convolutional neural network (CNN). We show that DP-DT effectively addresses the missing cone problem, which otherwise degrades the resolution and quality of standard 3D reconstruction algorithms. As DP-DT does not require pre-captured data or pre-training, it is not biased towards any particular dataset. Hence, it is a general technique that can be applied to a wide variety of 3D samples, including scenarios in which large datasets for supervised training would be infeasible or expensive. We applied DP-DT to obtain 3D RI maps of bead phantoms and complex biological specimens, both in simulation and experiment, and show that DP-DT produces higher-quality results than standard regularization techniques. We further demonstrate the generality of DP-DT, using two different scattering models, the first Born and multi-slice models. Our results point to the potential benefits of DP-DT for other 3D imaging modalities, including X-ray computed tomography, magnetic resonance imaging, and electron microscopy.
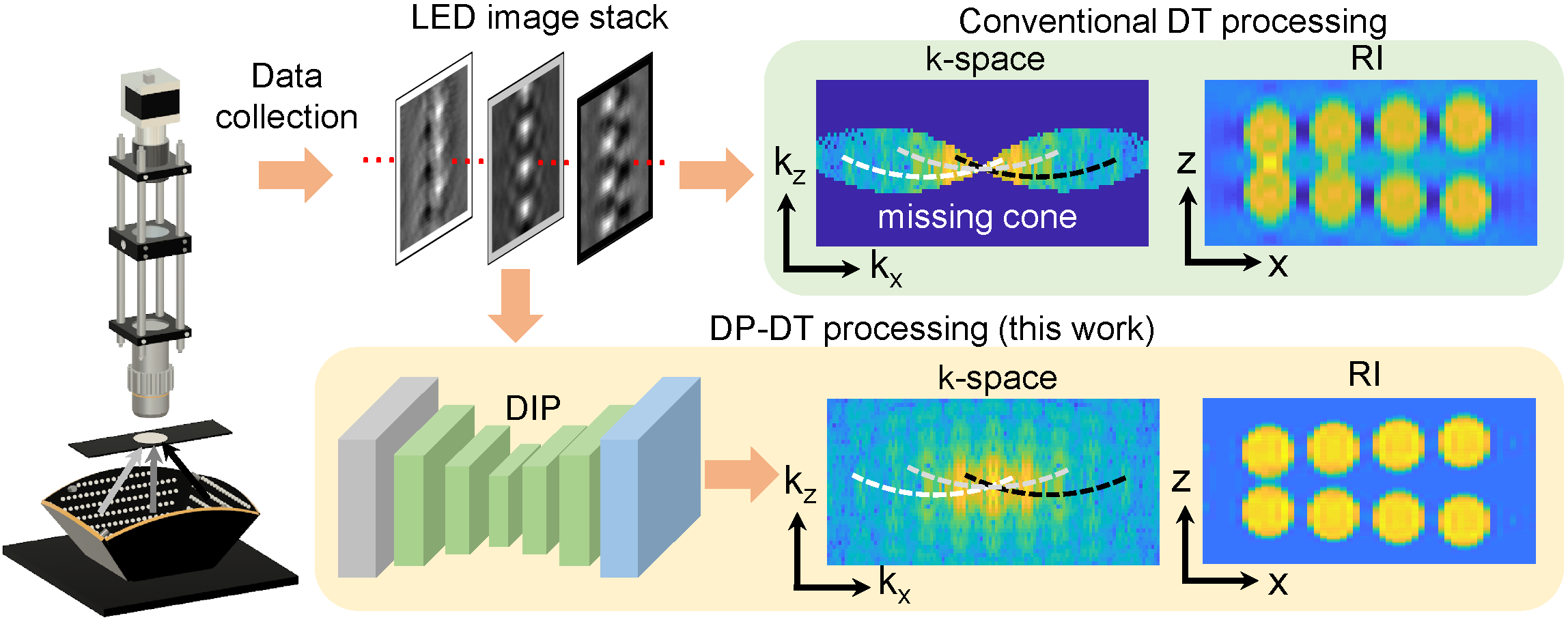
Overview
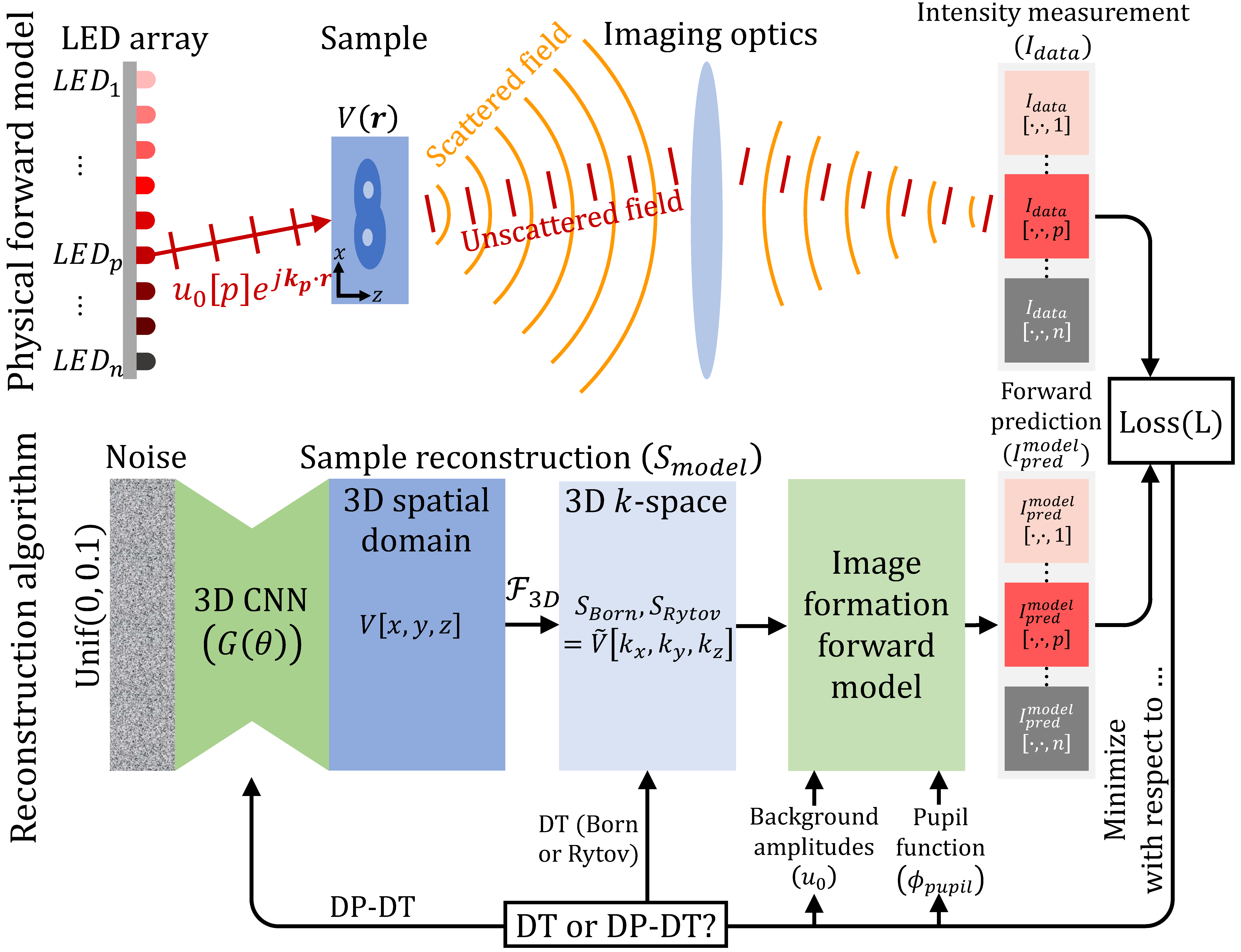
Our method, Deep Prior Diffraction Tomography (DP-DT), reparameterizes the 3D sample reconstruction as the output of an untrained convolutional neural network (CNN), which serves as the [deep image prior (DIP)](https://arxiv.org/abs/1711.10925). Thus, instead of optimizing the 3D reconstruction, we optimize the parameters of the CNN. At first glance, this may not seem to make a difference; after all, a CNN may have more parameters than the reconstruction itself. However, Ulyanov and colleagues have recently found that CNNs have an inherent preference for “natural” images, even without training, a bias which was demonstrated [on a variety of computer vision tasks](https://dmitryulyanov.github.io/deep_image_prior) such as digital super-resolution (not to be confused with optical super-resolution!), inpainting, and denoising.
We were intrigued by this result, and hypothesized that the DIP may be applied to fill in the missing cone in 3D diffraction tomography, which can be thought of as missing information in the Fourier domain that produces “unnatural” features in the real-space domain, especially in the z direction. Another way to think about this application is Fourier-domain inpainting. We confirmed this hypothesis empirically through a variety of samples, both simulated and experimental, which you can read about in our paper!
Sample results
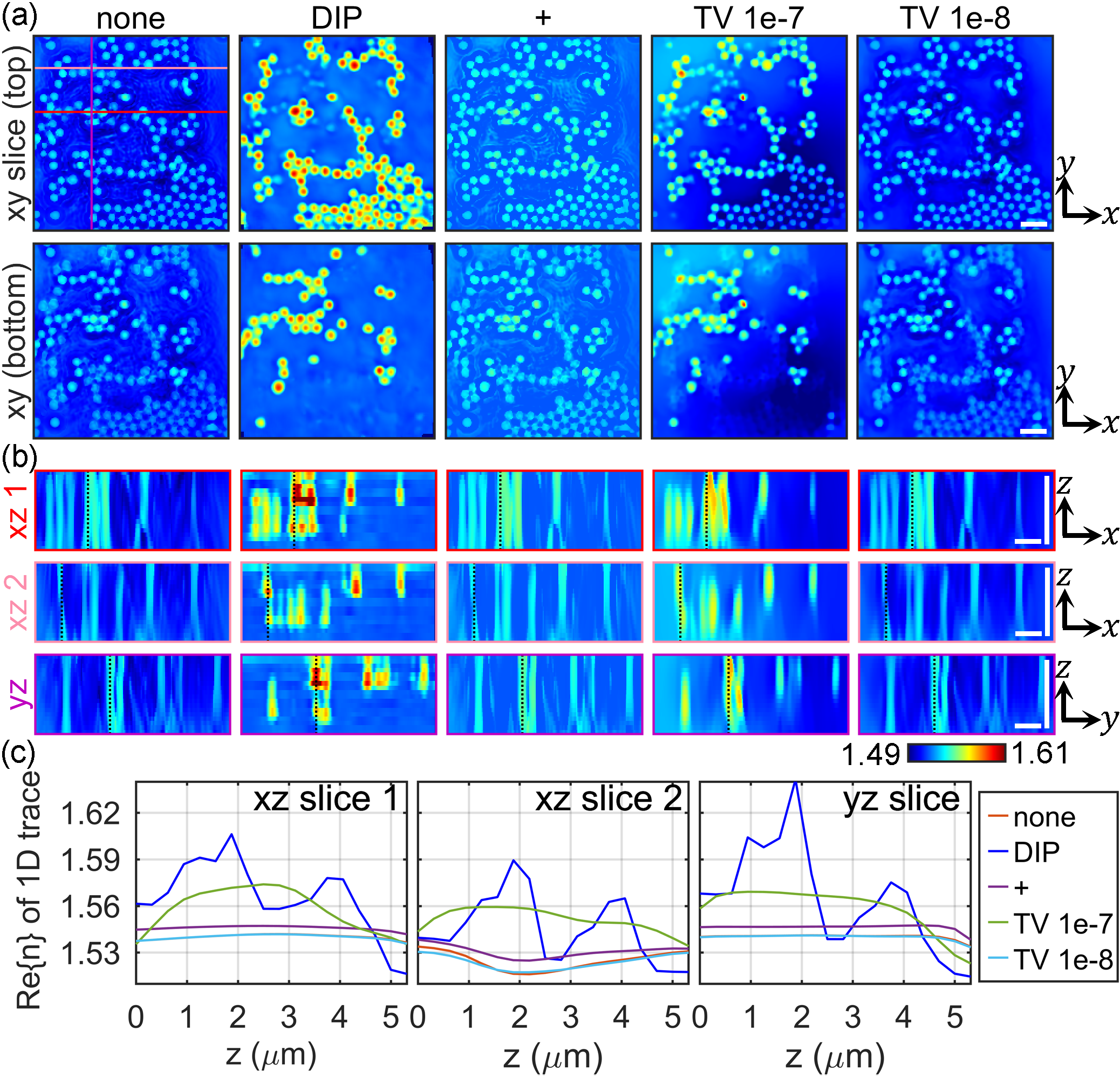
)
Here are are sample results from our paper (Fig. 10). We can see that using the DIP (DP-DT) produces superior results in this 2-layer polystyrene bead sample, compared to alternative regularization techniques like positivity (+) and total variation (TV). In particular, we can see better axial separation between the two layers with DP-DT, as well as refractive index values closer to the ground truth (1.59).
Code and data
We have open-sourced the code and datasets necessary to reproduce the experimental results figures in our paper (Figs. 7-10):
Code: Link to code
Datasets: Link to Dataset